от кой
=================
roncho
10.07.2022 19:11
| коментар
==========================================================================================
Не съм срещал точно това доказателство, но не е изключено да е написано от други хора.
От съвременна гледна точка това с векторите изглежда достатъчно просто.
За мен беше интересно как с първични знания древните постигали неща, които и
днес се изучават включително и от напреднали ученици. Понякога имам чувството, че
някога са знаели повече от запазеното до днес.
|
stancho
10.07.2022 06:52
| Дано е непознато това доказателство.
Полагаме за векторите AB=:a,BC=:b,AC=:c.
От правилото за събиране на вектори a+b=c.
Умножаваме скаларно двете страни на
равенството сами по себе си.
(a+b)^2=c^2 или
a^2+ab+ba+b^2=c^2.
Но ab=ba=0, защото двата вектора са перпендикулярни.
Тогава a^2+b^2=c^2.
|
biser190
06.05.2018 11:03
| Това чудо - Родоския Колос.Този фар в морето се е виждал на 20-40 километра разстояние по
море. На 40 километра разстояние фарът трябва да бъде скрит от 325,12 метра водна
„Изкривена" маса вода. Съществуват калкулатори в Интернет от различни източници, които...
|
roncho
29.05.2017 16:27
| @dehiksa
Благодаря за коментара. Изобщо казано, забележката се приема.
Премахнах изречението за комутативност.
Думата "комутативно" се ползва защото умножението вектор по число има такова свойство.
Думата "оператор" обаче предполага еднопосочност - първо се пише оператора,
след него - аргумента.
Възприетата дефиниция предполага, че операторът "grad" се прилага само
върху скаларно поле. Понятията "число" и "скалар" във физиката не са еднакви
- разбира се - но в този случай става дума за математически изрази, в които
скаларите и числата се третират еднакво.
|
dehiksa
02.05.2017 00:55
| Привет. Ако може да кажа и аз няколко думи относно страницата http://roncho.net/fiz/qm
/maxwell/nabla.htm
Добре би било да се спомене, че понятията, които се въвеждат, служат само за онагледяване
на изчисленията на градиент, ротор или дивергенция, и че това не е тяхната точна
математическа обосновка (която е доволно дълбока и интересна), тъй като, по начало,
операции като скаларно или векторно умножение на "вектори", чиито координати са различни
обекти, в математиката няма. Да не говорим, че по начало никой не казва какви обекти са
всъщност координатите на набла, на какво пространство от вектори е елемент набла, и
спрямо какъв базис са тези координати. Също така, думата скалар
не винаги означава число. Дивергенцията на векторно поле е функция, а не число (освен ако
не се пресмята в някоя точка). Но дори и на изложения формален език, (който за съжаление
в БГ си е останал стандартен), не може да се твърди, че операцията дивергенция е
комутативна. Забележете, че ако интерпретирате дивергеницята като някакво "скаларно"
произведение на "вектори", то като "умножавате" с набла отляво, получавате функция, а
като умножавате с набла от дясно, получавате диференциален оператор. Това са съвсем
различни обекти и не следва да се смесват.
|
vitef
07.12.2016 21:43
| Благодаря Ви! Чудесно написани материали.
|
Jordan
26.10.2016 22:22
| Благодаря ви много.
С вашата помощ успях да разбера какво е Вектор на Пойнтинг и "набла" операция , моите
уважения.
|
roncho
23.05.2011 21:31
| @stancho
Благодаря за забележките. Приемам ги безусловно. Май ще трябва да прибавя това пояснение
към статията "набла операции". Всичко което написа е необходимо и интуитивно усещах,
че трябва да бъде изложено по такъв начин, защото тези неща вече съм ги ползувал
на някои места без уточнения.
пп. Промених статията.
|
stancho
23.05.2011 13:39
| Страницата за оператора на Хамилтон е много добре написана.
Толкова добре, че се отказах да сложа своята.
Имам следните забележки
1. Добре е до се сномене че този оператор се нарича
"оператор на Хамилтон" и че набла е старинен музикален инструмент.
В моя вариант употребих изречението
"Да започнем да свирим".
2. Цитирам теорема от "Висша математика част 3" от
Спас Манолов и др. Държавно издателство Техника 1977 г. стр 124
"Ако операторът (набла) действа на произведение от две полета
u(M).v(M), u(M).F(M), F1(M).F2(M) или F1(M)xF2(M) то
той е равен на сумата от две събираеми, като в първото събираемо (набла)
действа на единия множител, а на другия не действа а във второто събираемо имаме обратното
".
С 0 в скоби означавам обекта, на който (набла) не действа.
Тогава нещата стоят така:
(набла)(F1xF2)=(набла)(F1xF2(0))+(набла)(F1(0)xF2)=
((набла)F1F2(0))+(набла)F1(0)F2)
{Тук тройката вектори се разбира като смесено произведение.
Използвайки свойствата му получаваме:}
((набла)xF1).F2(0)-F1(0).((набла)xF2))=
rot(F1).F2-F1.rot(F2)
3. div(rot(F)) е пример за двойно прилагане на (набла).
Добре е да се разгледат и другите случаи.
Пожелания за по-нататъшни успехи!
|
roncho
22.05.2011 14:00
| @stancho Приема се. Грешката е моя. Поправих равенството след 10, отляво махнах нулата
и допълних от дясно q4. Благодаря за прочитането и за корекцията.
Прочетох статията за Паскал от
http://ek.roncho.net/ElMath/Induction/Pascal/Pascal.html
в участъка "се наричат още биомни коефиценти" липсва буква н.
Написах програма, която изобразява по вертикала числата от триъгълника в плоскост n k.
Тя нарисува тази картинка при максимални n k = 50
и вертикален мащаб около 10-12
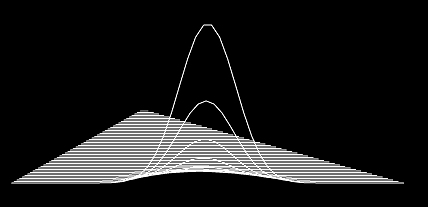
|
stancho
21.05.2011 19:11
| Прочетох за стълбата на Габриел.
Мисля, че нулата след формула 10 е излишна.
Не намерих за триъгълника на Паскал.
Моля те погледни новите страници в "математиката в училище".
Успехи!
|
roncho
14.05.2011 15:19
| Механизмът за писане на коментари от нови хора беше повреден.
Днес го поправих и вече работи.
Засега не е възможно към коментарите да се прилагат
картинки, но работя по този въпрос. Ще съобщя какво е станало.
Поздрави.
|
kalin
22.08.2010 16:21
| браво на Рьомер :)
|